Benchmarking OMol25-Trained Models on Experimental Reduction-Potential and Electron-Affinity Data
This preprint can also be viewed on ChemRxiv.
Introduction
In May 2025, Meta's Fundamental AI Research (FAIR) Chemistry team released Open Molecules 2025 (OMol25), a dataset of over one hundred million computational chemistry calculations at the ωB97M-V/def2-TZVPD level of theory.1 Along with it, the FAIR Chemistry team released several neural network potentials (NNPs) trained on the dataset, including models based on Meta's equivariant Smooth Energy Network (eSEN) architecture2 and a small and a medium version of a new Universal Model for Atoms (UMA).3
Since May, the OMol25-trained NNPs (OMol25 NNPs) have shown promising results in a variety of applications, often surpassing density-functional theory (DFT) and previous NNP methods in speed and accuracy.4,5 However, these models do not consider charge-based (Coulombic) interactions in their calculations. While OMol25 includes data about species in a variety of charge and spin states,1 the OMol25 NNPs do not consider the actual physics of charge or spin, potentially leading to inaccuracies when modeling long-range interactions.6–8 We reasoned that benchmarking these NNPs on charge- and spin-related chemical properties might be both interesting from a theoretical point of view and practically useful for practitioners seeking low-cost computational methods.
We selected two charge-related properties for benchmarking in this study: reduction potential, the voltage of an electrochemical cell in which the species in question gains one electron in a particular solvent, and electron affinity, the amount of energy released when the species in question gains one electron in the gas phase. Both properties quantify the change in energy for a process in which both the charge and spin multiplicity of a given species are changing, making them sensitive probes of charge- and spin-related accuracy. As pretrained NNPs that take both charge and spin as inputs and that can run calculations on structures with elements across the periodic table,1 the OMol25 NNPs are among the first NNPs capable of calculating the reduction potential and electron affinity of general main-group and organometallic species.
Here, we report the results of benchmarking three OMol25 NNPs—eSEN-OMol25-small-conserving (eSEN-S), UMA Small (UMA-S), and UMA Medium (UMA-M)—against experimental reduction-potential and electron-affinity data for various main-group and organometallic species. We also report the results of benchmarking certain DFT and semiempirical-quantum-mechanical (SQM) methods—all of which incorporate charge- and spin-based interactions—against the same experimental data.
Methods
Reduction Potential
We obtained experimental reduction-potential data from Neugebauer et al.,9 who compiled experimental reduction-potential data for 193 main-group species and 120 organometallic species (the data for structure 191 in the main-group set contained an error and was excluded from our study). For each species, the dataset included the charge and geometry of the non-reduced and reduced structures (optimized using GFN2-xTB10), the experimental reduction-potential value, and the identity of the solvent the experimental reduction potential was measured in.
We optimized the non-reduced and reduced structures of each species using each NNP. All geometry optimizations were run using geomeTRIC 1.0.2.11 We then input each optimized structure into the Extended Conductor-like Polarizable Continuum Solvation Model (CPCM-X)12 to obtain the structure's solvent-corrected electronic energy. By finding the difference between the electronic energy of the non-reduced structure (in electronvolts) and that of the reduced structure, we obtained a value equal to the predicted reduction potential of the species in question (in volts).
Neugebauer et al. also report the results of benchmarking several DFT and SQM methods against the experimental dataset; we compared the accuracy of the OMol25 NNPs on the experimental set to the accuracy of the B97-3c functional13 and the semiempirical GFN2-xTB model.10 In the Neugebauer paper, a shift of 4.846 eV is applied to all energy differences calculated using GFN2-xTB to correct for the self-interaction energy present in the GFNn-xTB methods.9 This correction was applied to all GFN2-xTB results throughout this paper.
We note that Neugebauer et al. use a slightly different procedure from the one used here: although we did not perform any conformer searches, Neugebauer et al. perform a conformer search on all main-group species using GFN2-xTB and the iMTD-GC algorithm. Additionally, they perform a thermostatistical energy correction, which includes zero-point vibrational energy corrections, on all structures. Rather than using CPCM-X to account for solvent effects, Neugebauer et al. use the implicit solvation models COSMO-RS (DFT), COSMO (PMx), and the Generalized Born model.
Electron Affinity
Chen and Wentworth report experimental gas-phase electron-affinity values for 37 simple main-group organic and inorganic species.14 Using the same procedure as above (without the solvent correction), we benchmarked the density functionals r2SCAN-3c15 and ωB97X-3c,16 the SQM models g-xTB17 and GFN2-xTB,10 and the OMol25 NNPs against this experimental dataset, thereby obtaining predicted electron-affinity values from seven methods. We did not benchmark g-xTB against the reduction-potential set because g-xTB does not yet support implicit solvent calculations. For certain calculations, a bond unrealistically broke upon addition of an electron to the initial structure; the results of these calculations were excluded from our analysis.
All density-functional-theory computations were conducted with Psi4 1.9.1.18 The default settings in Psi4 were modified somewhat: a (99, 590) integration grid with robust pruning, the Stratmann–Scuseria–Frisch quadrature scheme,19 and an integral tolerance of 10-14 were used throughout.20 Density fitting was employed for all calculations and a level shift of 0.10 Hartree was applied to accelerate SCF convergence.21
Rudshteyn et al. report experimental ionization energies for 11 organometallic coordination complexes.22 We obtained the electron affinity of the oxidized state of each complex by reversing the sign of the ionization energy. Using the same procedure as above (with no solvent correction), we benchmarked r2SCAN-3c, ωB97X-3c, g-xTB, GFN2-xTB, and the OMol25 NNPs against this set of experimental electron affinities.
Several structures from the Rudshteyn set failed to achieve self-consistent field convergence with ωB97X-3c. Second-order self-consistent field calculations were used for ωB97X-3c calculations that failed initially. If the second-order self-consistent field calculations also failed for a structure, then that structure was excluded from our analysis for ωB97X-3c.
Results
Reduction Potential
In our analysis, we separated the set of main-group species (termed OROP by Neugebauer et al.) from the set of organometallic species (termed OMROP). Figure 1 shows representative structures from the OROP set; Figure 2 shows the same for the OMROP set.
Figure 1: Representative examples of species in the main-group (OROP) reduction-potential set.
Figure 2: Representative examples of species in the organometallic (OMROP) reduction-potential set.
Statistics representing how accurately each method predicted experimental reduction potentials are shown in Table 1.
| Method | Set | MAE (V) | RMSE (V) | R2 |
|---|---|---|---|---|
| B97-3c | OROP | 0.260 (0.018) | 0.366 (0.026) | 0.943 (0.009) |
| OMROP | 0.414 (0.029) | 0.520 (0.033) | 0.800 (0.033) | |
| GFN2-xTB | OROP | 0.303 (0.019) | 0.407 (0.030) | 0.940 (0.007) |
| OMROP | 0.733 (0.054) | 0.938 (0.061) | 0.528 (0.057) | |
| eSEN-S | OROP | 0.505 (0.100) | 1.488 (0.271) | 0.477 (0.117) |
| OMROP | 0.312 (0.029) | 0.446 (0.049) | 0.845 (0.040) | |
| UMA-S | OROP | 0.261 (0.039) | 0.596 (0.203) | 0.878 (0.071) |
| OMROP | 0.262 (0.024) | 0.375 (0.048) | 0.896 (0.031) | |
| UMA-M | OROP | 0.407 (0.082) | 1.216 (0.271) | 0.596 (0.124) |
| OMROP | 0.365 (0.038) | 0.560 (0.064) | 0.775 (0.053) |
Table 1: Mean absolute error (MAE), root mean squared error (RMSE), and coefficient of determination (R2) values representing the accuracy of reduction-potential calculations on the main-group (OROP, N=192) and organometallic (OMROP, N=120) datasets (note that the B97-3c and GFN2-xTB calculations were performed by Neugebauer et al.), with the standard error of each statistic shown in parentheses.
The OMol25 NNPs performed less accurately on the main-group reduction-potential set than both B97-3c and GFN2-xTB. Among the OMol25 NNPs, UMA-S performed significantly better than both UMA-M and eSEN-S on main-group reduction potentials; both UMA-M and eSEN-S struggled with outliers, resulting in RMSE values over 1 V. UMA-S performed similarly to GFN2-xTB on OROP; all low-cost methods were noticeably less accurate than B97-3c for main-group species.
Organometallic complexes like those found in OMROP can have complex electronic structure and are often challenging to model with low-cost quantum-chemical methods; consistent with this, both B97-3c and GFN2-xTB were significantly less accurate on the OMROP set than on the OROP set. In contrast, the OMol25 NNPs modeled organometallic reduction potentials more accurately than main-group reduction potentials (see Figure 3). All three OMol25 NNPs performed better than at least one of B97-3c and GFN2-xTB on the OMROP dataset; as before, UMA-S was the most accurate.
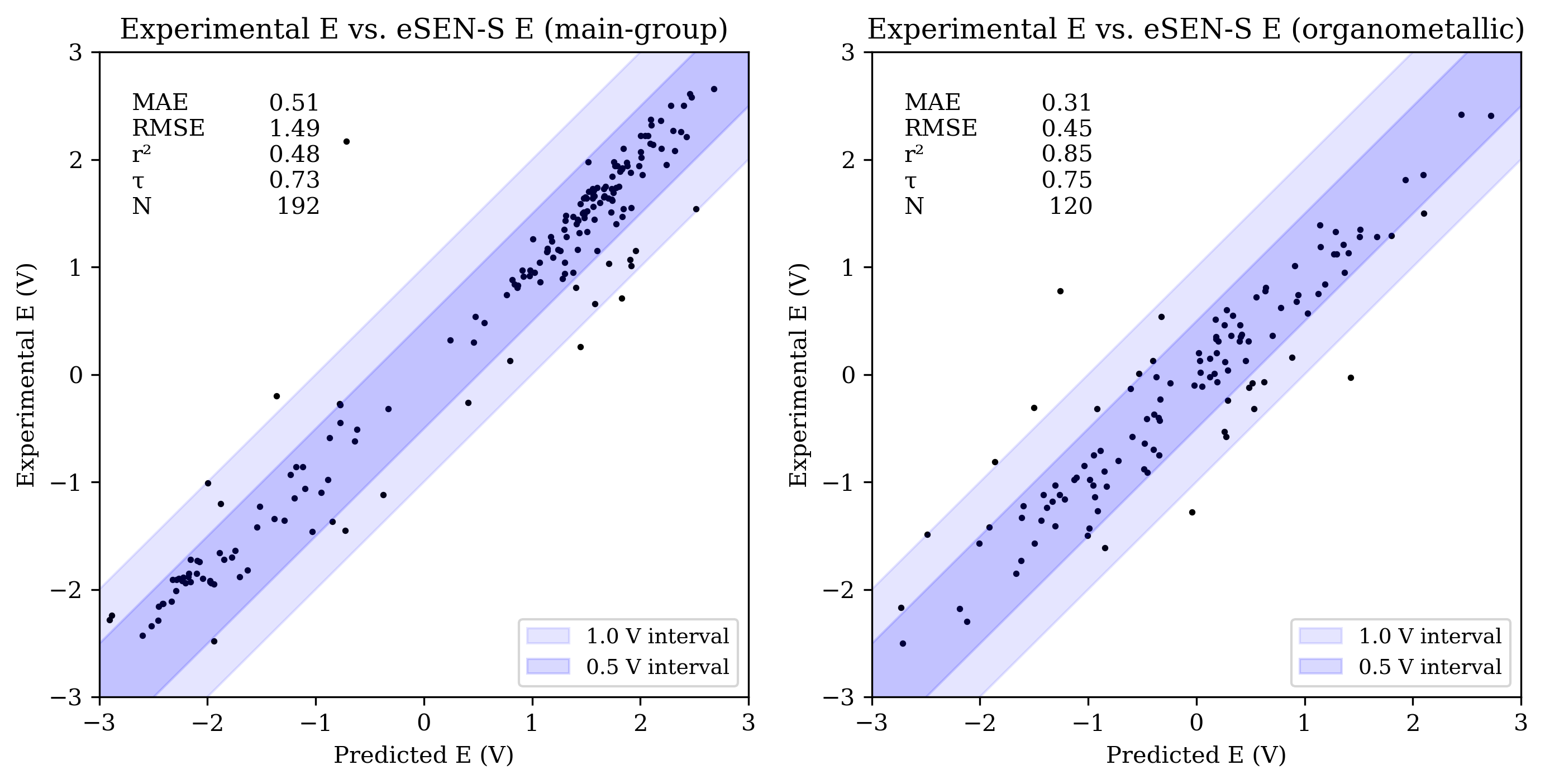
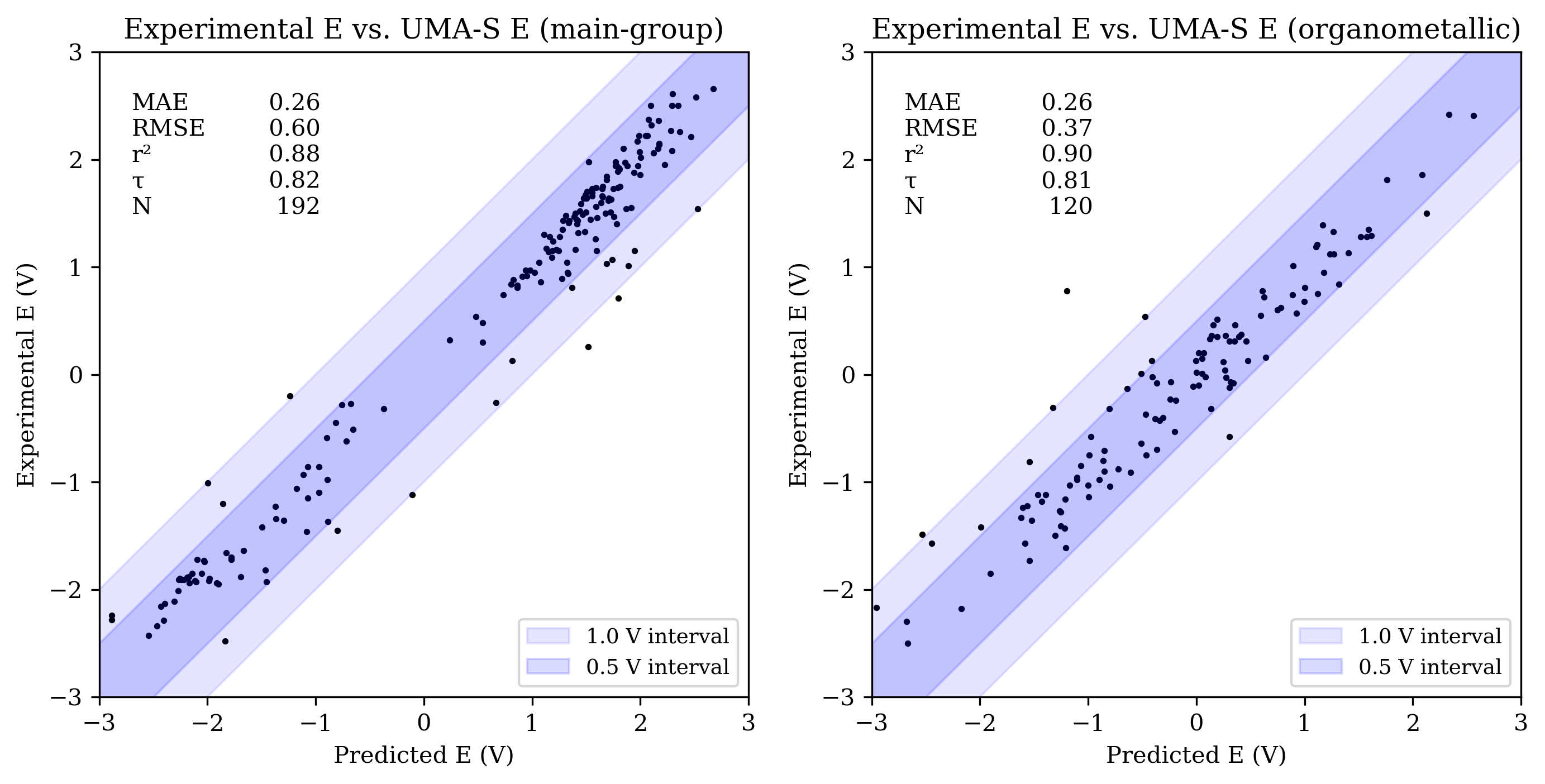
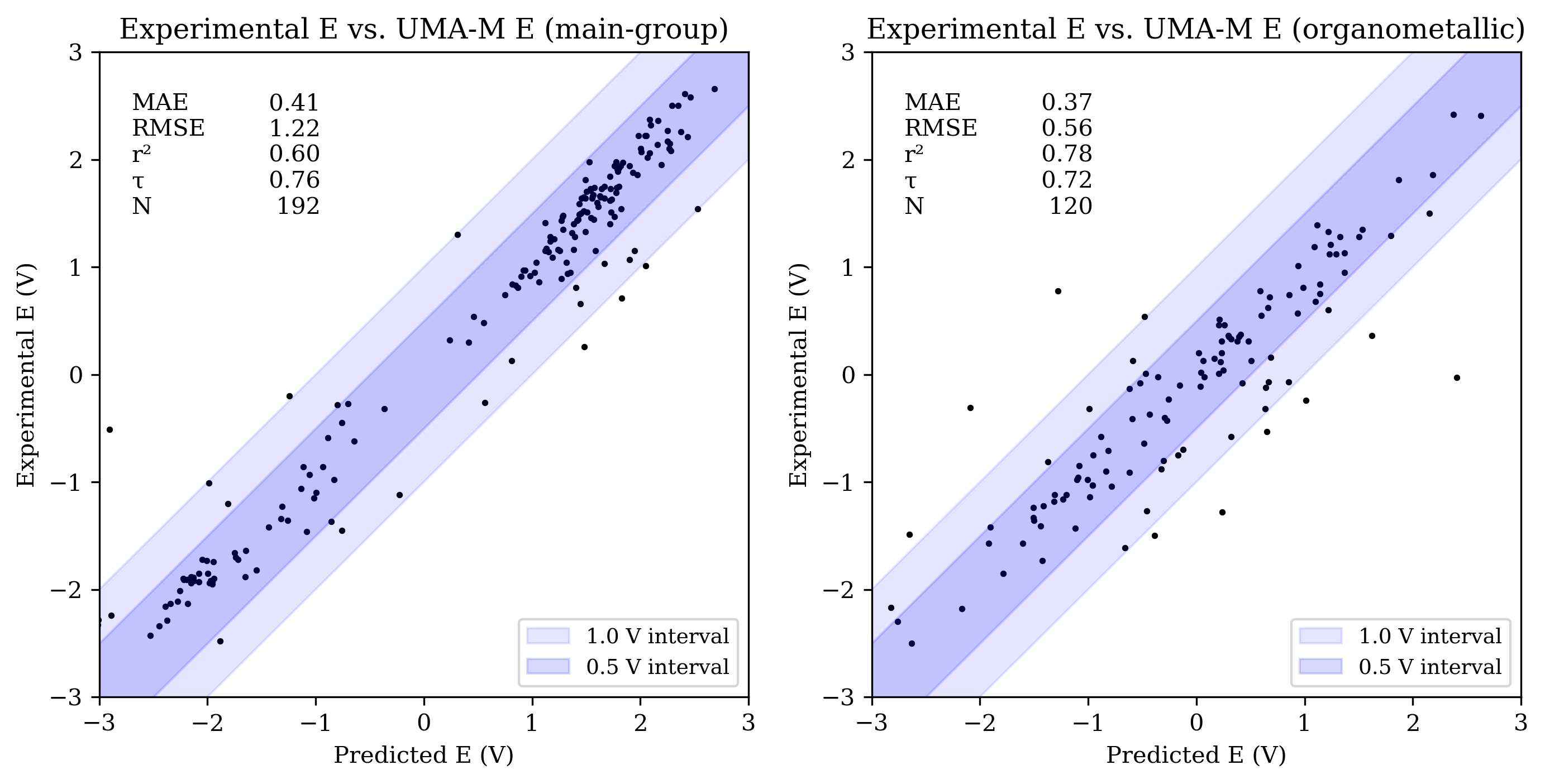
Figure 3: Scatterplots of experimental reduction potential vs. predicted reduction potential for eSEN-S (top), UMA-S (middle), and UMA-M (bottom). Each panel shows data for main-group (left) and organometallic (right) sets (only −3 V to +3 V shown). For each set, the mean absolute error (MAE), root mean squared error (RMSE), coefficient of determination (R2), Kendall rank correlation coefficient (τ), and number of values (N) are shown.
Electron Affinity
Statistics representing how accurately each method predicted experimental electron affinities are shown in Table 2.
| Method | Set | MAE (V) | RMSE (V) | R2 |
|---|---|---|---|---|
| r2SCAN-3c | MG | 0.466 (0.071) | 0.626 (0.081) | 0.845 (0.050) |
| OM | 0.340 (0.069) | 0.412 (0.072) | 0.988 (0.006) | |
| ωB97X-3c | MG | 0.467 (0.076) | 0.651 (0.086) | 0.785 (0.087) |
| OM | 0.591 (0.263) | 0.918 (0.386) | 0.945 (0.091) | |
| g-xTB | MG | 0.470 (0.079) | 0.662 (0.110) | 0.833 (0.060) |
| OM | 0.714 (0.270) | 1.150 (0.441) | 0.839 (0.128) | |
| GFN2-xTB | MG | 0.600 (0.099) | 0.838 (0.118) | 0.630 (0.121) |
| OM | 0.849 (0.241) | 1.167 (0.296) | 0.873 (0.060) | |
| eSEN-S | MG | 0.502 (0.082) | 0.701 (0.111) | 0.716 (0.089) |
| OM | 0.245 (0.057) | 0.309 (0.061) | 0.983 (0.011) | |
| UMA-S | MG | 0.439 (0.077) | 0.637 (0.097) | 0.754 (0.077) |
| OM | 0.261 (0.083) | 0.382 (0.109) | 0.984 (0.009) | |
| UMA-M | MG | 0.398 (0.078) | 0.615 (0.101) | 0.787 (0.076) |
| OM | 0.167 (0.036) | 0.205 (0.041) | 0.993 (0.003) |
Table 2: Mean absolute error (MAE), root mean squared error (RMSE), and coefficient of determination (R2) values representing the accuracy of electron-affinity calculations on the main-group (MG, N=37) and organometallic (OM, N=11) datasets, with the standard error of each statistic shown in parentheses.
All levels of theory performed similarly on the main-group electron-affinity dataset reported by Chen and Wentworth (≈0.6–0.8 V RMSE). In contrast, predicted organometallic electron affinities were significantly more accurate with the OMol25 NNPs than with physics-based methods. While physics-based methods generally predicted electron affinities with worse absolute accuracy for the organometallic dataset, the OMol25 NNPs predicted organometallic electron affinities significantly more accurately than they predicted main-group electron affinities.
The poor performance of low-cost composite DFT methods on the organometallic electron-affinity dataset prompted us to evaluate different levels of theory. Using geometries optimized at the GFN2-xTB level of theory, we benchmarked various DFT functionals and basis sets against the set of organometallic electron affinities. We found that several other functionals and basis sets also achieved a 0.2–0.4 V RMSE, similar to the OMol25-trained NNPs (Table 3). While a full benchmark of quantum-chemical methods for electron-affinity prediction is beyond the scope of this work, this survey shows that the accuracy achieved by the OMol25 NNPs is within the expected range for DFT calculations.
| Functional | Basis set | MAE (V) | RMSE (V) | R2 |
|---|---|---|---|---|
| B3LYP-D3BJ | def2-SVP | 0.244 | 0.308 | 0.993 |
| def2-TZVP | 0.212 | 0.286 | 0.991 | |
| def2-TZVPP | 0.214 | 0.291 | 0.991 | |
| def2-TZVPPD | 0.235 | 0.312 | 0.988 | |
| B97-D3BJ | def2-SVP | 0.294 | 0.375 | 0.993 |
| def2-TZVP | 0.287 | 0.346 | 0.991 | |
| def2-TZVPP | 0.273 | 0.342 | 0.991 | |
| def2-TZVPPD | 0.273 | 0.326 | 0.991 | |
| M06 | def2-SVP | 0.399 | 0.709 | 0.954 |
| def2-TZVP | 0.410 | 0.695 | 0.953 | |
| def2-TZVPP | 0.412 | 0.696 | 0.953 | |
| def2-TZVPPD | 0.205 | 0.260 | 0.991 |
Table 3: Accuracy of organometallic electron-affinity calculations for several density functionals and basis sets: mean absolute error (MAE), root mean squared error (RMSE), and coefficient of determination (R2) are shown.
Discussion and Conclusions
Accurate prediction of reduction potentials and electron affinities requires a theoretical method to simultaneously account for the effects of changing molecular charge and spin multiplicity. Since the OMol25-trained NNPs consider neither charge- nor spin-based physics, using them to predict these properties might reasonably be expected to yield poor results. Nevertheless, the OMol25 NNPs generally perform equivalently to or better than state-of-the-art semiempirical or low-cost DFT methods on the benchmark sets studied here. These results suggest that a lack of explicit physics does not significantly compromise OMol25 NNPs' ability to optimize and determine the energetics of structures in a variety of charge states for small systems. This study does not address condensed-phase effects or scaling to large systems; there may be emergent inaccuracies that arise from the lack of explicit physics at larger length scales.
Despite the significant improvements reported for UMA-M over UMA-S in the original UMA report,3 including for charge- and spin-related properties, we did not see consistent improvement here. In fact, UMA-S performed significantly better than UMA-M on main-group reduction potentials.
While low-cost DFT and semiempirical methods are known to give less accurate predictions for organometallic complexes than for organic or main-group compounds, the OMol25-trained NNPs here perform better for organometallic species than for main-group compounds. This may arise in part from the high level of theory used to generate the OMol25 dataset: ωB97M-V is known to describe organometallic chemistry with better accuracy than low-cost DFT methods like those benchmarked here, and this accuracy seems to be inherited by the models trained on OMol25.23 Still, the fact that the NNPs describe the behavior of electronically complex organometallic species more accurately than the behavior of simple closed-shell main-group molecules is puzzling and merits further study.
The success of the OMol25-trained NNPs at predicting reduction potentials and electron affinities for chemically diverse systems implies that these models can be used for zero-shot prediction of charge-related properties. Our results show that NNPs can predict these properties with comparable or superior accuracy to conventional low-cost quantum-chemical methods. We anticipate that these NNPs will be useful in high-throughput virtual screening of redox-flow electrolytes, photoredox catalysts, and other electroactive materials.
Acknowledgements
The authors thank Jonathon Vandezande and Arien Wagen for helpful discussions.
Bibliography
- Levine, D. S.; Shuaibi, M.; Spotte-Smith, E. W. C.; Taylor, M. G.; Hasyim, M. R.; Michel, K.; Batatia, I.; Csányi, G.; Dzamba, M.; Eastman, P.; et al. The Open Molecules 2025 (OMol25) Dataset, Evaluations, and Models. arXiv, May 13, 2025. DOI: 10.48550/arXiv.2505.08762
- Fu, X.; Wood, B. M.; Barroso-Luque, L.; Levine, D. S.; Gao, M.; Dzamba, M.; Zitnick, C. L. Learning Smooth and Expressive Interatomic Potentials for Physical Property Prediction. arXiv April 23, 2025. DOI: 10.48550/arXiv.2502.12147
- Wood, B. M.; Dzamba, M.; Fu, X.; Gao, M.; Shuaibi, M.; Barroso-Luque, L.; Abdelmaqsoud, K.; Gharakhanyan, V.; Kitchin, J. R.; Levine, D. S.; et al. UMA: A Family of Universal Models for Atoms. arXiv, June 30, 2025. DOI: 10.48550/arXiv.2506.23971
- Vandezande, J.; Wagen, C. ExpBDE54: A Slim Experimental Benchmark for Exploring the Pareto Frontier of Bond-Dissociation-Enthalpy-Prediction Methods. ChemRxiv, July 21, 2025. DOI: 10.26434/chemrxiv-2025-4s082
- Gharakhanyan, V.; Yang, Y.; Barroso-Luque, L.; Shuaibi, M.; Levine, D. S.; Michel, K.; Bernat, V.; Dzamba, M.; Fu, X.; Gao, M.; et al. FastCSP: Accelerated Molecular Crystal Structure Prediction with Universal Model for Atoms. arXiv, August 4, 2025. DOI: 10.48550/arXiv.2508.02641
- Anstine, D. M.; Isayev, O. Machine Learning Interatomic Potentials and Long-Range Physics. The Journal of Physical Chemistry A 2023, 127, 11, 2417–2431. DOI: 10.1021/acs.jpca.2c06778
- Unke, O. T.; Chmiela, S.; Sauceda, H. E.; Gastegger, M.; Poltavsky, I.; Schütt, K. T.; Tkatchenko, A.; Müller, K.-R. Machine Learning Force Fields. Chemical Reviews 2021, 121, 16, 10142–10186. DOI: 10.1021/acs.chemrev.0c01111
- Wagen, C. Long-Range Forces and Neural Network Potentials. Blog, August 16, 2025. https://corinwagen.github.io/public/blog/20250816_long_range_forces_and_nnps.html
- Neugebauer, H.; Bohle, F.; Bursch, M.; Hansen, A.; Grimme, S. Benchmark Study of Electrochemical Redox Potentials Calculated with Semiempirical and DFT Methods. The Journal of Physical Chemistry A 2020, 124, 35, 7166–7176. DOI: 10.1021/acs.jpca.0c05052
- Bannwarth, C.; Ehlert, S.; Grimme, S. GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions. Journal of Chemical Theory and Computation 2019, 15, 3, 1652–1671. DOI: 10.1021/acs.jctc.8b01176
- Wang, L.-P.; Song, C. Geometry Optimization Made Simple with Translation and Rotation Coordinates. The Journal of Chemical Physics 2016, 144, 21, 214108. DOI: 10.1063/1.4952956
- Stahn, M.; Ehlert, S.; Grimme, S. Extended Conductor-like Polarizable Continuum Solvation Model (CPCM-X) for Semiempirical Methods. The Journal of Physical Chemistry A 2023, 127, 33, 7036–7043. DOI: 10.1021/acs.jpca.3c04382
- Brandenburg, J. G.; Bannwarth, C.; Hansen, A.; Grimme, S. B97-3c: A Revised Low-Cost Variant of the B97-D Density Functional Method. The Journal of Chemical Physics 2018, 148, 6, 064104. DOI: 10.1063/1.5012601
- Chen, E. C. M.; Wentworth, W. E. Experimental Determination of Electron Affinities of Organic Molecules. Molecular Crystals and Liquid Crystals Incorporating Nonlinear Optics 1989, 171, 1, 271–285. DOI: 10.1080/00268948908065801
- Grimme, S.; Hansen, A.; Ehlert, S.; Mewes, J.-M. r²SCAN-3c: A “Swiss Army Knife” Composite Electronic-Structure Method. The Journal of Chemical Physics 2021, 154, 6, 064103. DOI: 10.1063/5.0040021
- Müller, M.; Hansen, A.; Grimme, S. ωB97X-3c: A Composite Range-Separated Hybrid DFT Method with a Molecule-Optimized Polarized Valence Double-ζ Basis Set. The Journal of Chemical Physics 2023, 158, 1, 014103. DOI: 10.1063/5.0133026
- Froitzheim, T.; Müller, M.; Hansen, A.; Grimme, S. g-xTB: A General-Purpose Extended Tight-Binding Electronic Structure Method for the Elements H to Lr (Z = 1–103). ChemRxiv June 24, 2025. DOI: 10.26434/chemrxiv-2025-bjxvt
- Turney, J. M.; et al. Psi4: an open-source ab initio electronic structure program. WIREs Computational Molecular Science 2012, 2, 556–565. DOI: 10.1002/wcms.93
- Stratmann, R. E.; Scuseria, G. E.; Frisch, M. J. Achieving Linear Scaling in Exchange–Correlation Density Functional Quadratures. Chemical Physics Letters 1996, 257, 213–223. DOI: 10.1016/0009-2614(96)00600-8
- Gray, M.; Bowling, P. E.; Herbert, J. M. Comment on “Benchmarking Basis Sets for Density Functional Theory Thermochemistry Calculations: Why Unpolarized Basis Sets and the Polarized 6-311G Family Should Be Avoided”. The Journal of Physical Chemistry A 2024, 128, 7739–7745. DOI: 10.1021/acs.jpca.4c00283
- Saunders, V. R.; Hillier, I. H. A “Level-Shifting” Method for Converging Closed Shell Hartree–Fock Wave Functions. International Journal of Quantum Chemistry 1973, 7, 699–705. DOI: 10.1002/qua.560070407
- Rudshteyn, B.; Weber, J. L.; Coskun, D.; Devlaminck, P. A.; Zhang, S.; Reichman, D. R.; Shee, J.; Friesner, R. A. Calculation of Metallocene Ionization Potentials via Auxiliary Field Quantum Monte Carlo: Toward Benchmark Quantum Chemistry for Transition Metals. Journal of Chemical Theory and Computation 2022, 18, 5, 2845–2862. DOI: 10.1021/acs.jctc.1c01071
- Santra, G.; Martin, J. M. L. Some Observations on the Performance of the Most Recent Exchange–Correlation Functionals for the Large and Chemically Diverse GMTKN55 Benchmark. Proceedings of ICCMSE-2019. AIP Publishing, 2019. DOI: 10.1063/1.5137915